Nonlinear Measurements of Heart Rate Variability

From Schrödinger's (1944) perspective, life is aperiodic (e.g., oscillations occur without a fixed period) and fluctuates between randomness and periodicity.

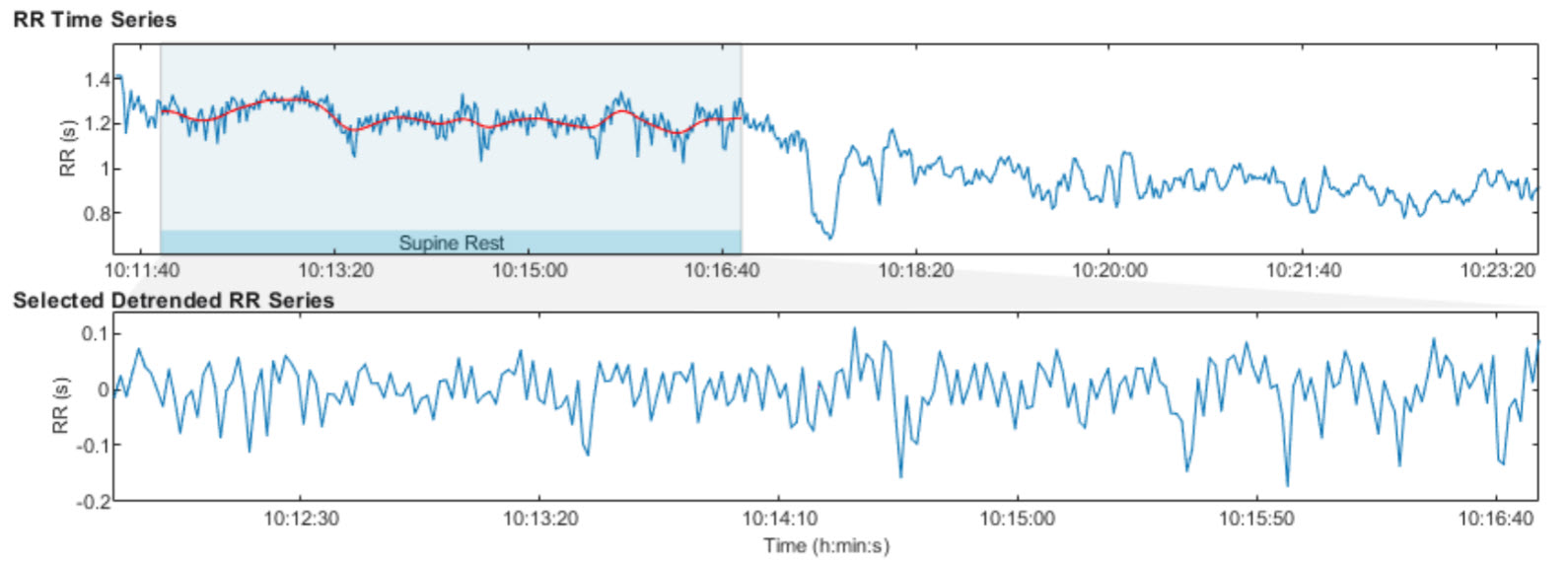
Twenty-four-hour ECG monitoring yields a time series of R-R intervals (time between successive heartbeats). The graphic below is from Tarvainen and Niskanen (2023).




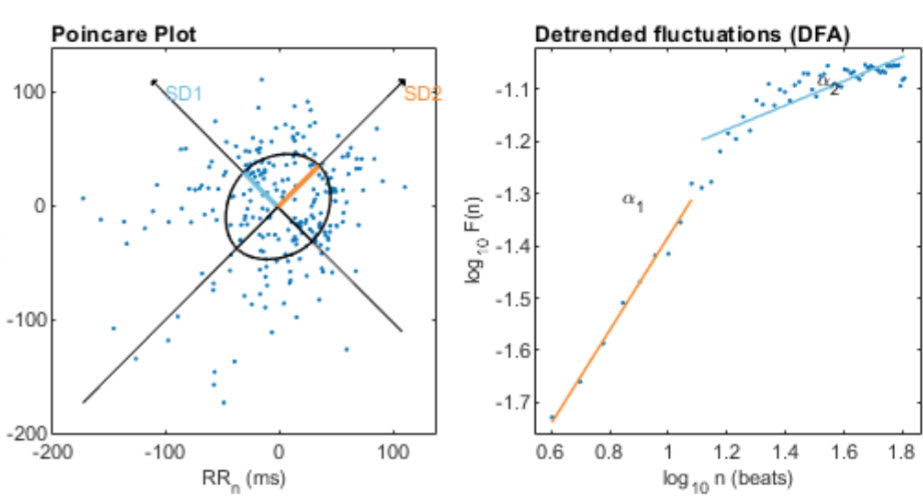
Nonlinearity means that a relationship between variables cannot be plotted as a straight line. Poincaré and detrended fluctuation analysis plots illustrate nonlinear HRV. The graphic below is from Tarvainen and Niskanen (2023).




Nonlinear measurements allow us to quantify the unpredictability of a time series, which results from the complexity of the mechanisms that regulate heart rate variability. Nonlinear indices correlate with specific frequency and time domain measurements when the same processes generate them. While stressors and disorders like diabetes can depress some nonlinear metrics, elevated values do not always signal health. For example, in post-myocardial infarction (post-MI) patients, increased nonlinear HRV is an independent risk factor for mortality (Stein et al., 2005).

Karemaker (2020) observed that HRV entropy measures have yielded few practical applications and are not consistently superior to time- and frequency-domain measurements:

Comparisons between more classical statistical- or frequency analysis derived- and entropy-derived measures do, however, not always favor the newer ones (Zhang et al., 2013). This may, partly, be due to the fact that in many applications, entropy-measurements require rather long recordings before reaching a stable value. In critical situations this is a serious drawback. However, when the requirement of more time and more data points it is not an issue, entropy analysis may be a viable option to dig deeper in the complexities of the heart rate signal at hand.

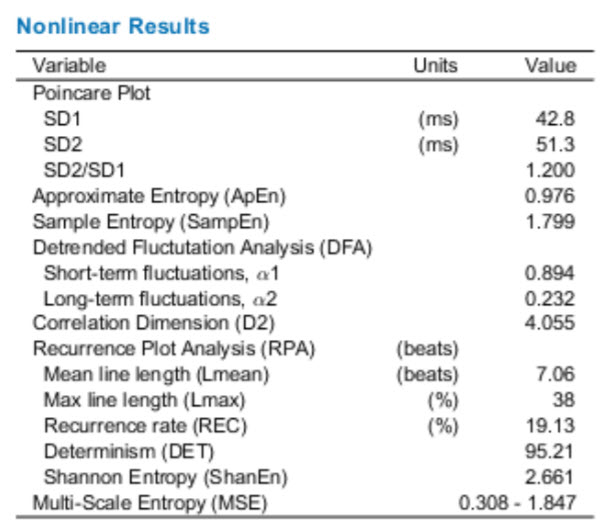
The graphic below shows nonlinear HRV metrics from the Kubios manual (Tarvainen & Niskanen, 2020).

BCIA Blueprint Coverage

BCIA's HRV Biofeedback Blueprint does not cover nonlinear metrics.




This unit covers Poincaré plots, S, SD1, SD2, SD1/SD2, Approximate Entropy (ApEn), Sample Entropy (SampEn), Multiscale Entropy (MSE), Detrended Fluctuation Analysis (DFA), α1 and α2, and Correlation Dimension.

Please click on the podcast icon below to hear a full-length lecture.

Poincaré plot

A Poincaré plot (return map) is graphed by plotting every R-R interval against the prior interval, creating a scatter plot. Poincaré plot analysis allows researchers to visually search for patterns buried within a time series (a sequence of successive values). The example below is courtesy of SWHarden.com. Unlike frequency-domain measurements, Poincaré plot analysis is insensitive to changes in trends in the R-R intervals (Behbahani et al., 2012).

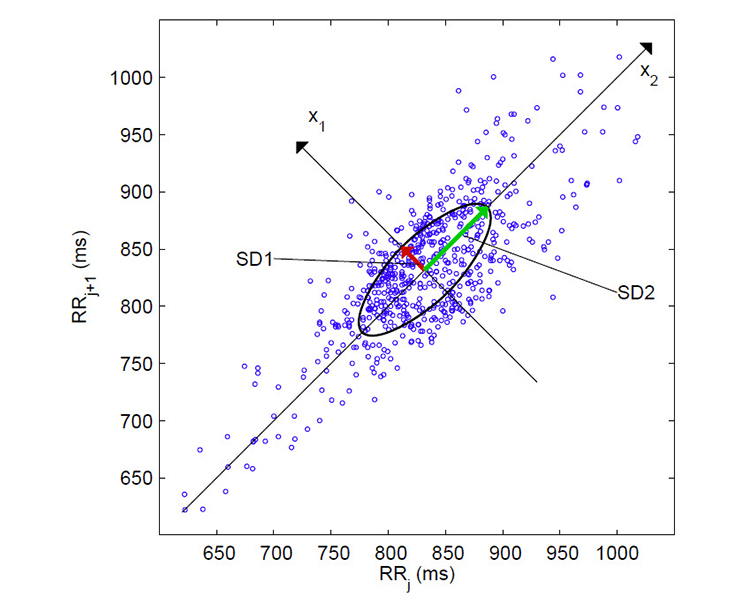
S, SD1, SD2, and SD1/SD2

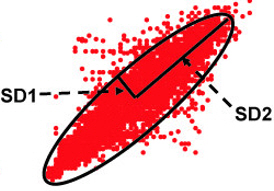
We can analyze a Poincaré plot by fitting an ellipse (curve which resembles a squashed circle) to the plotted points. After fitting the ellipse, we can derive three nonlinear measurements, S, SD1, and SD2.

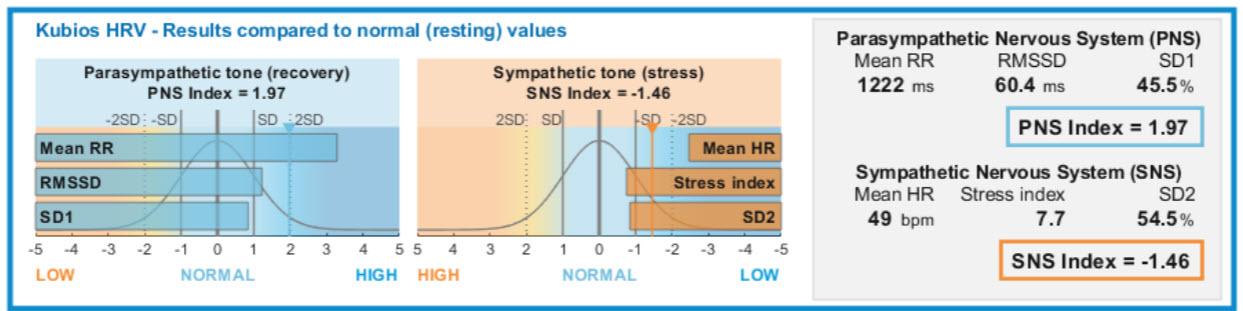
Baroreflex Sensitivity is correlated with S, SD1, and SD2 nonlinear HRV indices.

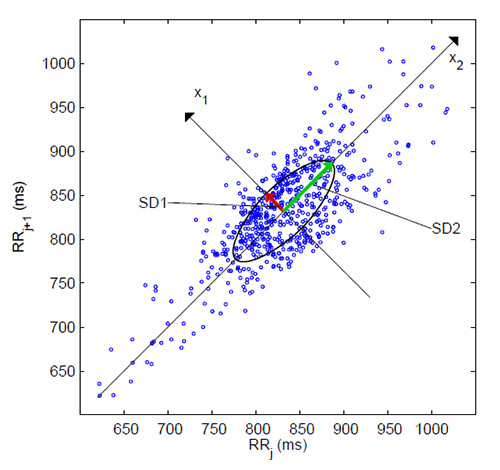
The ratio of SD1/SD2, which measures the unpredictability of the R-R time series, is used to measure autonomic balance when the monitoring period is sufficiently long, and there is sympathetic activation. SD1/SD2 is correlated with the LF/HF ratio (Behbahani et al., 2012; Guzik et al., 2012). The Poincaré plot below is from Tarvainen and Niskanen (2012).

Approximate Entropy

Approximate entropy (ApEn) measures the regularity and complexity of a time series. ApEn was designed for brief time series in which some noise may be present and makes no assumptions regarding underlying system dynamics (Kuusela, 2013). Applied to HRV data, large ApEn values indicate low predictability of fluctuations in successive R-R intervals (Beckers, Ramaekers, & Aubert, 2001). Small ApEn values mean the signal is regular and predictable (Tarvainen & Niskanen, 2012).

Sample Entropy

Sample entropy (SampEn) was designed to provide a less biased and more reliable signal regularity and complexity measure than ApEn (Lippman et al., 1994). SampEn values are more stable than ApEn for the same participant over successive days (Richman & Moorman, 2000). SampEn values are interpreted and used like ApEn and may be calculated from a much shorter time series of fewer than 200 values (Kuusela, 2013).

Multiscale Entropy

Multiscale Entropy (MSE) extends entropy analysis using resampling to increase the time series' data points to reveal slower fluctuations (Costa et al., 2002, 2005).

The tabled values below are from Tarvainen and Niskanen (2020).

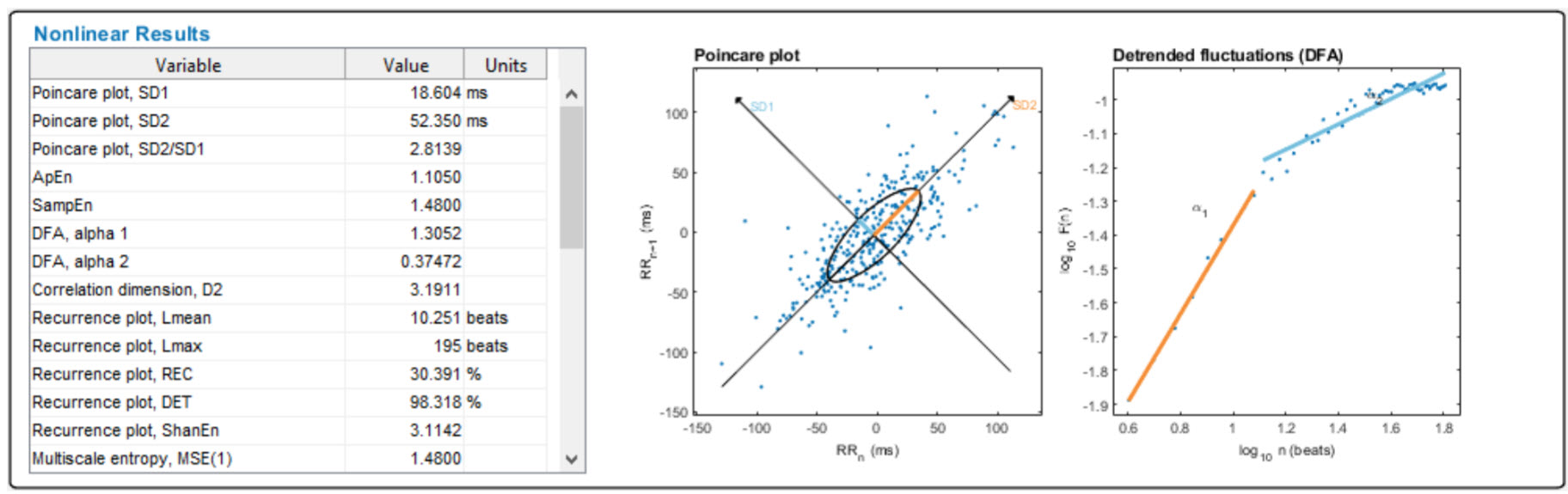
Detrended Fluctuation Analysis (DFA)

Detrended fluctuation analysis (DFA) extracts the correlations between successive R-R intervals over different time scales. This analysis results in slope α1, which represents short-term fluctuations, and slope α2, which describes long-term fluctuations. The short-term correlations extracted using DFA reflect the baroreceptor reflex, while long-term correlations reflect the regulatory mechanisms limiting the beat cycle's fluctuation. DFA is designed to analyze a time series that spans several hours of data (Kuusela, 2013).

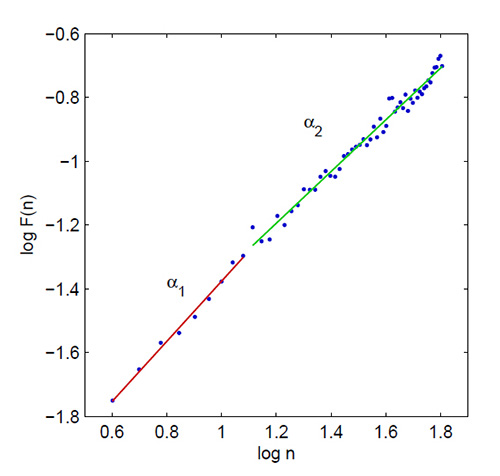
Correlation Dimension

The correlation dimension estimates the minimum number of variables required to construct a system dynamics model. The more variables needed to predict the time series, the greater its complexity.

The correlation dimension allows us to construct a system dynamics model using the fewest predictor variables.

An attractor, depicted below, is a set of values towards which a variable in a dynamic system converges over time. Graphic © zentilia/Shutterstock.com.




The correlation dimension measures a system's attractor dimension, which can be an integer or fractal (Kuusela, 2013). Below is a correlation dimension plot.

Summary Table

If nonlinear measurements of HRV are reduced in diseases like diabetes, is increased nonlinearity always desirable?

No. The answer depends on which processes generate the nonlinearity. While increased nonlinear HRV measurements could signal improved health in a diabetic client with better glucose control, it could signal a greater risk of death in a post-MI patient.

Glossary

aperiodic: oscillations have no fixed period.

approximate entropy (ApEn): a nonlinear index of HRV that measures the regularity and complexity of a time series.

attractor: a set of values towards which a variable in a dynamic system converges over time.

attractor dimension: the number of variables required to model a dynamic system.

correlation dimension: nonlinear index of HRV that estimates the minimum number of variables required to construct a model of the studied system.

detrended fluctuation analysis (DFA): nonlinear index of HRV that extracts the correlations between successive R-R intervals over different time scales and yields estimates of short-term (α1) and long-term (α2) fluctuations.

ellipse: a curve that resembles a squashed circle, fitted to a Poincaré plot to calculate nonlinear HRV measurements SD1, SD2, SD1/SD2.

interbeat interval: the time interval between the peaks of successive R-spikes (initial upward deflections in the QRS complex). An IBI is also called the NN (normal-to-normal) interval after removing artifacts.

multiscale entropy (MSE): an extension of ApEn that uses resampling to increase the number of data points in a time series to detect slower fluctuations.

nonlinear measurements: indices that quantify the unpredictability of a time series, which results from the complexity of the mechanisms that regulate the measured variable.

nonlinearity: a relationship between variables that cannot be plotted as a straight line.

Poincaré plot analysis (PPA): a visual display that plots every R-R interval against the prior interval, creating a scatterplot to identify patterns buried within a time series.

R-R interval: time between consecutive heartbeats, also called the interbeat interval (IBI), measured in milliseconds.

S: a nonlinear index of HRV that measures the area of the ellipse, which represents total HRV.

sample entropy (SampEn): a nonlinear index of HRV that was designed to provide a less biased measure of signal regularity and complexity than ApEn.

SD1: the standard deviation of the distance of each point from the y = x-axis that measures short-term HRV.

SD2: the standard deviation of each point from the y = x + average RR interval that measures short- and long-term HRV.

SD1/SD2: a ratio that measures the unpredictability of the R-R time series and autonomic balance under appropriate monitoring conditions.

time series: a sequence of successive values. For example, a 24-hour record of R-R intervals.

Test Yourself

Click on the ClassMarker logo to take 10-question tests over this unit without an exam password.

REVIEW FLASHCARDS ON QUIZLET

Click on the Quizlet logo to review our chapter flashcards.

Visit the BioSource Software Website

BCIA offers two HRV Biofeedback Certification paths: Biofeedback and Neurofeedback. For Biofeedback, BioSource Software offers Human Physiology to satisfy BCIA's Human Anatomy & Physiology requirement. For Neurofeedback, BioSource provides Physiological Psychology to satisfy BCIA's Physiological Psychology requirement.

BCIA has accredited each course, and they combine affordable pricing ($150) with industry-leading content.

Assignment

Now that you have completed this module, explain the difference between linear and nonlinear relationships. When might greater nonlinear HRV values be worrisome?

Acknowledgment

This article draws heavily on graphics published in Tarvainen and Niskanen's Kubios HRV User's Guide.

References

Beckers, F., Ramaekers, D., & Aubert, A. E. (2001). Approximate entropy of heart rate variability: Validation of methods and application in heart failure. Cardiovascular Engineering: An International Journal, 1(4), 177-182. http://dx.doi.org/10.1023/A:1015212328405

Behbahani, S., Dabanloo, N. J., & Nasrabadi, A. M. (2012). Ictal heart rate variability assessment with focus on secondary generalized and complex partial epileptic seizures. Advances in Bioresearch, 4(1), 50-58.

Brennan, M., Palaniswami, M., & Kamen, P. (2001). Do existing measures of Poincaré plot geometry reflect nonlinear features of heart rate variability? IEEE Trans Biomed Eng, 48(11), 1342-1347. https://doi.org/10.1109/10.959330

Brennan, M., Palaniswami, M., & Kamen, P. (2002). Poincaré plot interpretation using a physiological model of HRV based on a network of oscillators. Am J Physiol Heart Circ Physiol, 283, H1873-H1886. https://doi.org/10.1152/ajpheart.00405.2000

Carrasco, S., Caitán, R., González, R., & Yánez, O. (2001). Correlation among Poincaré plot indexes and time and frequency domain measures of heart rate variability. J Med Eng Technol, 25(6), 240-248. https://doi.org/10.1080/03091900110086651

Ciccone, A. B., Siedlik, J. A., Wecht, J. M., Deckert, J. A., Nguyen, N. D., & Weir, J. P. (2017). Reminder: RMSSD and SD1 are identical heart rate variability metrics. Muscle Nerve. https://doi.org/10.1002/mus.25573

Costa, M., Goldberger, A. L., & Peng, C. K. (2002). Multiscale entropy analysis of complex physiologic time series. Physical Rev. Lett. 89, 068102. https://doi.org/10.1103/physrevlett.89.068102

Costa, M., Goldberger, A. L., & Peng, C. K. (2005). Multiscale entropy analysis of biological signals. Physical Rev. E, 71,021906. https://doi.org/10.1103/physreve.71.021906

Guzik P., Piskorski, J., Krauze, T., & Wysocki, H. (2012), The influence of changing respiratory rate on HRV is portrayed by descriptors of Poincaré analysis. Unpublished manuscript obtained from ResearchGate.

Huikuri, H. V., Mäkikallio, T. H., Raatikainen, P., Perkiömäki, J., Castellanos, A., & Myerburg, R. J. (2003), Prediction of sudden cardiac death: Appraisal of the studies and methods assessing the risk of sudden arrhythmic death. Circulation, 108(1), 110-115. https://doi.org/10.1161/01.cir.0000077519.18416.43

Kuusela, K. (2013). Methodological aspects of heart rate variability analysis. In M. V. Kamath, M. A. Watanabe, & A. R. M. Upton (Eds.). Heart rate variability (HRV) signal analysis. CRC Press.

Lake, D. E., Richman, J. S., Griffin, M. P., & Moorman, J. R. (2002). Sample entropy analysis of neonatal heart rate variability. ajp, 283, R789-R797. https://doi.org/10.1152/ajpregu.00069.2002

Lippman, N., Stein, K. M., & Lerman, B. B. (1994). Comparison of methods for removal of ectopy in measurement of heart rate variability. Am J Physiol, 267(1 Pt 2), H411-H4118. https://doi.org/10.1152/ajpheart.1994.267.1.h411

Perkiomaki, J. S., Zareba, W., Badilini, F., & Moss, A. J. (2002). Influence of atropine on fractal and complexity measures of heart rate variability. ANE, 7(4), 326-330. https://doi.org/10.1111/j.1542-474x.2002.tb00181.x

Richman, J. A., & Moorman, J. R. (2000). Physiological time-series analysis using approximate entropy and sample entropy. Am J Physiol, 278, H2039-H2049. https://doi.org/10.1152/ajpheart.2000.278.6.h2039

Schrödinger, E. (1944). What is life? The physical aspect of the living cell.

Stein, P. K., Domitrovich, P. P., Huikuri, H. V., & Kleiger, R. E. (2005). Traditional and nonlinear heart rate variability are each independently associated with mortality after myocardial infarction. J Cardiovasc Electrophysiol, 16(1), 13-20. https://doi.org/10.1046/j.1540-8167.2005.04358.x

Tarvainen, M. P., & Niskanen, J.-P. (2020). Kubios HRV version 3.4 user's guide. : University of Finland.

Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology (1996). Heart rate variability: Standards of measurement, physiological interpretation, and clinical use. Circulation, 93, 1043-1065.

Tulppo, M. P., Makikallio, T. H., Seppanen, T., Laukkanen, R. T., & Huikuri, H. V. (1998). Vagal modulation of heart rate during exercise: Effects of age and physical fitness. Am J Physiol, 274, H424-H429. https://doi.org/10.1152/ajpheart.1998.274.2.h424

Tulppo, M. P., Makikallio, T. H., Takala, T. E., Seppanen, T., & Huikuri, H. V. (1996). Quantitative beat-to-beat analysis of heart rate dynamics during exercise. Am J Physiol, 271, H244-H252. https://doi.org/10.1152/ajpheart.1996.271.1.h244

Zhang, Y., de Peuter, O. R., Kamphuisen, P. W., & Karemaker, J. M. (2013). Search for HRV-parameters that detect a sympathetic shift in heart failure patients on ß-blocker treatment. Front. Physiol. 4, 81. https://doi.org/10.3389/fphys.2013.00081